Description
“Phenomena and Drag Originating From The Boundary Layer”
Part 3 of the series “The Science of Sailing” is dedicated to the topic of viscous drag. Viscous drag is the prime component of hydrodynamic drag for most sailing craft (and most other boats and ships). Its assessment is still surrounded by notions and assumptions that are at best only partially correct – notwithstanding the fact that the study of this subject has been ongoing since William Froude presented his paper entitled: “The Fundamental Principles which Govern the Behaviour of Fluids, with Special Reference to the Resistance of Ships”, in 1875.
Viscous drag originates from the boundary layer, the thin layer of fluid flow around a body in which the velocity of the flow is decelerated to zero (relative to the velocity of the body) at the body surface, over a very small distance. Fluid viscosity is here manifest to a very significant degree, opposing this deceleration, causing significant shear forces between adjacent layers of the fluid, and a skin friction force on the surface of the body, that varies along its length. The summation of this skin friction force along the body leads to its friction drag which, for most vessels, is the most important component of total drag. Aspects of the boundary layer that are of importance for the understanding of viscous drag are considered in detail in Section 7.2 of this book.
Viscous drag is composed of two primary components: friction drag and viscous pressure drag. Friction drag is generally assessed on the basis of expressions for the friction drag of smooth flat plates, which are semi-empirical in nature. The friction drag obtained from a selection of these expressions (see Table 7.2) varies by 11.9% at a Reynolds number of one million, and as much as 18.3% at a Reynolds number of 1000 million, as described in Section 7.3. I have addressed this disturbing state of affairs in Section 7.5 by adopting the results of RANS CFD calculations for five geometrically-similar hulls of different length, each for 6 values of the Froude number, and identified the flat plate friction drag formulation that displays the same trend with Reynolds number as found from these CFD calculations. In so-doing, I discovered that a flaw exists in the formulation of this particular friction drag formulation, for low values of the Reynolds number, which I have rectified by offering an alternative formulation. This study of the friction drag of the three-dimensional hull of typical sailing yachts (and many other slender hull forms) revealed that, generally, it is less than that of the equivalent flat plate (the plate with the same length and wetted area as the subject hull).
Another aspect that has needed examination for some time is the practise of adopting a form factor to account for the excess viscous drag of a hull relative to the friction drag of the equivalent flat plate. The viscous pressure drag is an important part of this excess viscous drag. The present-day method for determining the value of this form factor for a particular hull (described in Section 6.6.4 of Part 2) is based on the limiting value of the total drag-to-flat plate friction drag ratio, as the Froude number approaches zero. While this value of the form factor is strictly only applicable for zero Froude number (i.e. to those cases when the body is deeply submerged or high in the air), it is actually applied for non-zero values of the Froude number as well (i.e. also to those cases when the body is at, or near, the air-water interface). There is no scientific basis for this practise, but it is widely utilized because of the ease by which an estimate is obtained for the viscous drag by simply multiplying the friction drag of the equivalent flat plate by a factor. However, viscous pressure drag consists of two parts. The first of these is the Reynolds-dependent part which is indeed found on considering the limit of the total drag-to-friction drag ratio as the froude number approaches zero, which part conforms to the viscous pressure drag as found in wind tunnels when testing foil sections and such. The second part is the viscous pressure drag associated with wave-making. This last part, in contemporary ship hydrodynamics, is all but forgotten when the form factor used is based on this condition. It is then lumped into the so-called residual drag, obtained by subtracting the flat plate friction drag (multiplied by the adopted value of the form factor) from the total drag, which is generally scaled (from model to prototype for example) by adopting Froude’s Law of Comparison, in which no account is made for the variation of this component with Reynolds number.
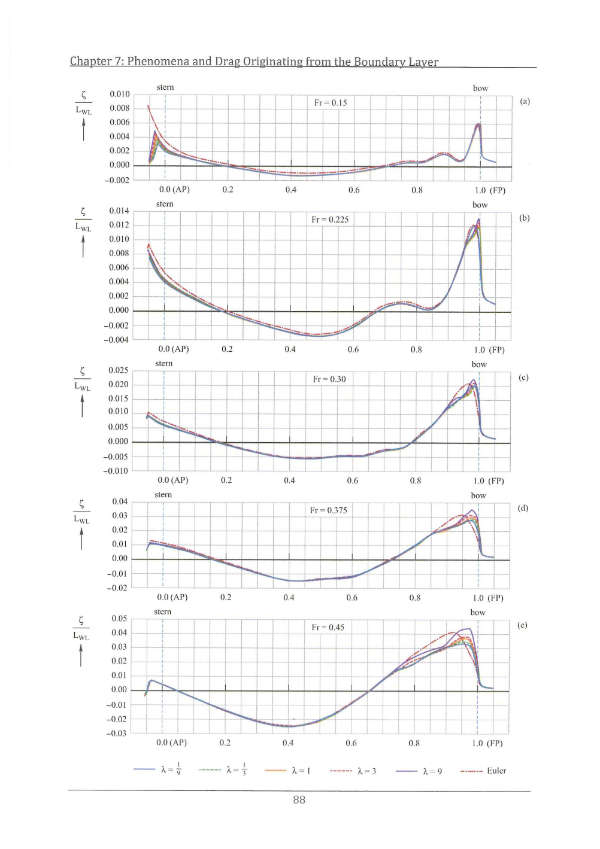
By again adopting the results of a large series of CFD results, for both the RANS and the Euler options of the FINETM/Marine code, the magnitude of both components of viscous pressure drag were identified for the same series of sailing yacht hulls referred to earlier. This involved the comparison of the pressure drag as found from the RANS CFD calculations (for the case when viscosity plays its part in resolving the flow around the hull) with the pressure drag as obtained from the “Euler” calculations (for the case when viscosity is set equal to zero). The result of subtracting the Euler result from the RANS result defines the viscous pressure drag. As described in Section 7.9, this component of viscous drag was found to be dominantly negative, quickly annulling the positive component of viscous pressure drag found for the “Froude approaches zero” condition, which is further addressed in Section 7.10. Comparison of the waves generated in both cases reveals that fluid viscosity causes a reduction in wave elevation. The resulting level of total viscous drag is thus lower than that generally assumed, and the wave drag (equal to the pressure drag as found from the Euler calculations) higher than contemporary methods lead us to believe. These findings have particular consequences for the method in use today for the scaling of drag between hulls of different size. The most important aspect of a scaling procedure in ship hydrodynamics is the level of drag assigned as viscous (Reynolds number dependent) and non-viscous (Froude number dependent) because each is scaled differently. This is discussed in detail in Section 7.11. Contemporary scaling methods assign too much drag to the viscous category, the outcome of which is generally a too optimistic prediction of total drag when based on the drag of a smaller version of the subject hull (such as its model). The use of a form factor based on the limiting Froude condition clearly leads to errors. Viscous drag rarely exceeds that of the friction drag of the equivalent flat plate, unless the hull exhibits flow separation.
Part 3 of “The Science of Sailing” defines a new methodology for a reliable prediction of viscous- and wave drag. This methodology requires the use of both a RANS and an “Euler” calculation with a refined CFD code.
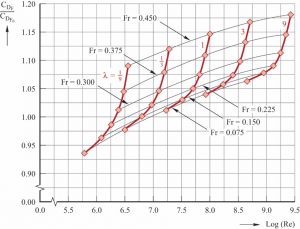
Figure 7.30: Graphs of the value of the friction drag coefficient (from CFD), divided by the friction drag coefficient of the equivalent flat plate according to the 1957 ITTC formulation (7.3.11), for the hull of a sailing yacht at five different scales, for six values of the Froude number. The five scale factors are 1/9, 1/3, 1, 3, and 9. The Froude numbers are 0.075, 0.15, 0.225, 0.30, 0.375, and 0.45. The coefficient values are based on the wetted area of the stationary hull. This figure reveals that the slope of the 1957 ITTC formulation is in error as there is no reason why the slope of these curves should increase as the length of these hulls increases.
Prices exclude 9% value added tax, for orders outside of The Netherlands we do not calculate tax. For shipping and administration cost we calculate €6,95 for The Netherlands and €14,95 outside of The Netherlands.
Attention! If you wish to order from outside the Netherlands OR more than one book please use this form.